有効数字について

　2004年7月23日　村田

１．             有効数字とは

　理工学で扱う数値は多くの場合測定値であり，測定方法によって精度が決まっています．つまりある程度の誤差を含んでいるということです．例えば長さであれば，ものさし，ノギス，レーザー変位計などを用いて測ります．

　さて，ある長さの測定値をLとして，以下の二つの数値の書き方を比べてみましょう．

 

　　　L=105.4mm　 (1)

     　　 L=105.40mm　(2)

 

　式(1)の場合には小数点以下第１位の”4”までが意味のある測定値であるのに対し，式(2)の場合には小数点以下第２位の”0”までが意味のある測定値であることを示します．つまり式(2)では小数点以下第２位の数値は1でも2でも3でもなく0であることを明記しているのです．最後の桁がゼロだからといって書くのを省略してしまうのは大きな誤りです．

　このように測定によって得られた意味のある数値のことを「有効数字」と呼びます．

　式(1)では有効数字は４桁，式(2)では５桁となります．（このことを有効桁数が４桁（または５桁）と言う場合もあります．）

　皆さんが理工学で扱う数値はほとんどが単位を有する物理量であり，何らかの測定によって得られた値です．これらの数値を表示するときには意味のある数字（有効数字）だけを表示するように気をつけましょう．

 

例）　1mと1.00mは異なります．1mの場合には有効数字１桁，つまり0.1mの桁の数値は測定できなかった（わからない）ということです．

 

 

２．有効数字を考慮した測定値の計算方法

２．１　和（足し算）と差（引き算）の有効数字

　測定値は，測定精度に応じた有効数字を持っていますので，その測定値を使って計算するときにも有効数字を意識した計算方法を用いる必要があります．電卓（またはパソコンでエクセル）に数値を入力して表示された結果を全ての桁数書くのは誤りです．

　例えば，質量1.00kgの物体Aと質量0.2kgの物体Bの合計質量を計算してみましょう．最後の有効桁の次の桁を”？”で書いてみると以下のようになります．

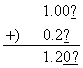
　ここで不確かな値には下線をつけて表示しました．小数点以下第２位での”0”と”？”との足し算の結果はやはり不確かな数値なので下線をつけた”0”で表しています．

　つまり，足し算（引き算）では小数点を揃えて計算をし，最後の桁の位取りが最も高いものに合わせて有効数字を決めることになります．この場合には合計質量は1.2kgと有効数字２桁で表示するのが正しい結果です．

 

２．２　積（掛け算）と商（割り算）の有効数字

　さて，掛け算や割り算の場合はどうなるのでしょうか？

　例えば，長方形の面積を計算するときに長辺の長さが55.4mm，短辺の長さが9.3mmだとしましょう．

足し算の場合と同様に最後の有効桁の次の桁を”？”で書いてみると以下のようになります．

 

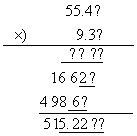
最初の各辺の長さの”？”はその桁を四捨五入して有効数字の最後の桁が出てきたと考えることができます．上の計算では掛け算での桁の繰り上がりも考慮して不確かな数値を下線で表示しています．（最初の”  ?? ??”では頭の 100の位まで下線がついていることに注意．）

よって最後の結果の１の位の5を四捨五入して5.2x10² mm²と有効数字２桁とするのが正しいことがわかります．つまり掛け算や割り算の場合には計算結果の有効桁数は最も有効数字の少ない数値の有効桁数と等しくなります．

 

 

２．３      実際の計算での有効数字に関する注意事項

 

・     最終的に必要な有効桁数よりも一桁多くとって計算する．

 

計算に与えられた数値の最も少ない有効桁数が２桁の場合に途中の計算結果まで全て有効数字２桁にまとめてしまうと最終結果での計算による誤差が大きくなってしまいます．計算途中では最終的に必要な有効桁数よりも一桁多くとって計算するようにしましょう．

また，円周率や重力加速度などの値を何桁目まで使うかについても同様に最終的に必要な有効桁数よりも一桁多くとって計算するのが正しい計算方法です．

 

・     測定値とそうでない値を区別する．

 

例えば円周の長さを半径の測定値Rと円周率πとを使って表すと，

（円周の長さ）＝2πR

となります．ここで”2”は半径から直径を計算するための係数で，測定値ではなく小数点以下に無限にゼロが続く正確な数値だと考えられます．このような正確な数値は小数点以下を明記せずに（有効数字を考えずに）表記することができます．

 

・     途中で有効数字が少なくなる場合（引き算）に注意．

 

前述の通り，足し算（引き算）では小数点を揃えて計算をし，最後の桁の位取りが最も高いものに合わせて有効数字を決めます．例えば21.2℃と20.0℃の温度差を計算する場合を考えてみましょう．温度差は21.2−20.0=1.2℃となります．つまりここで有効数字が３桁から２桁に減少してしまいました．20.3℃と20.0℃の温度差であれば20.3−20.0=0.3℃となり，この場合には有効数字１桁になります．熱量の計算では比熱と温度差の積をとりますので，数値の有効数字が全て３桁で与えられていても，温度差の計算の部分で有効数字が２桁または１桁に減少することがあることに注意する必要があります．もちろんこの場合には結果としての熱量の有効数字は２桁または１桁となります．

　　

以上．